PID controller หัวใจของระบบควบคุมทางอุตสาหกรรม ซึ่งเป็นอะไรที่จำเป็นอย่างยิ่งสำหรับช่างเทคนิคและวิศวกร หรือเปรียบเสมือนอาวุธประจำกายชนิดหนึ่งของวิศวกรหรือช่างเทคนิคที่ทำงานเกี่ยวข้องกับระบบควบคุมอุตสาหกรรม ดังนั้นหากใครลืม (หรือคืนอาจารย์ไปหมดแล้ว) ก็ทบทวนหรือรีเฟรชกันใหม่ได้ หรือหากถ้ายังไม่เคยรู้จักหรือเข้าใจมาก่อนก็ติดตามได้ดังต่อไปนี้
PID controller
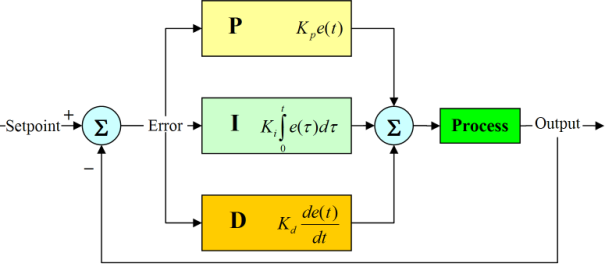
ระบบควบคุมแบบสัดส่วน-ปริพันธ์-อนุพันธ์ (อังกฤษ: PID controller) เป็นระบบควบคุมแบบป้อนกลับที่ใช้กันอย่างกว้างขวาง ซึ่งค่าที่นำไปใช้ในการคำนวณเป็นค่าความผิดพลาดที่หามาจากความแตกต่างของตัว แปรในกระบวนการและค่าที่ต้องการ ตัวควบคุมจะพยายามลดค่าผิดพลาดให้เหลือน้อยที่สุดด้วยการปรับค่าสัญญาณขา เข้าของกระบวนการ ค่าตัวแปรของ PID ที่ใช้จะปรับเปลี่ยนตามธรรมชาติของระบบ
วิธีคำนวณของ PID ขึ้นอยู่กับสามตัวแปรคือค่าสัดส่วน, ปริพันธ์ และ อนุพันธ์ ค่าสัดส่วนกำหนดจากผลของความผิดพลาดในปัจจุบัน, ค่าปริพันธ์กำหนดจากผลบนพื้นฐานของผลรวมความผิดพลาดที่ซึ่งพึ่งผ่านพ้นไป, และค่าอนุพันธ์กำหนดจากผลบนพื้นฐานของอัตราการเปลี่ยนแปลงของค่าความผิดพลาด น้ำหนักที่เกิดจากการรวมกันของทั้งสามนี้จะใช้ในการปรับกระบวนการ
โดยการปรับค่าคงที่ใน PID ตัวควบคุมสามารถปรับรูปแบบการควบคุมให้เหมาะกับที่กระบวนการต้องการได้ การตอบสนองของตัวควบคุมจะอยู่ในรูปของการไหวตัวของตัวควบคุมจนถึงค่าความผิด พลาด ค่าโอเวอร์ชูต (overshoots) และ ค่าแกว่งของระบบ (oscillation) วิธี PID ไม่รับประกันได้ว่าจะเป็นระบบควบคุมที่เหมาะสมที่สุดหรือสามารถทำให้กระบวน การมีความเสถียรแน่นอน
การประยุกต์ใช้งานบางครั้งอาจใช้เพียงหนึ่งถึงสองรูปแบบ ขึ้นอยู่กับกระบวนการเป็นสำคัญ พีไอดีบางครั้งจะถูกเรียกว่าการควบคุมแบบ PI, PD, P หรือ I ขึ้นอยู่กับว่าใช้รูปแบบใดบ้าง
การควบคุมแบบ PID ได้ชื่อตามการรวมกันของเทอมของตัวแปรทั้งสามตามสมการ:
MV(t) = Pout + Iout + Dout
เมื่อ
- Pout , Iout และ Dout เป็นผลของสัญญาณขาออกจากระบบควบคุม PID จากแต่ละเทอมซึ่งนิยามตามรายละเอียดด้านล่าง
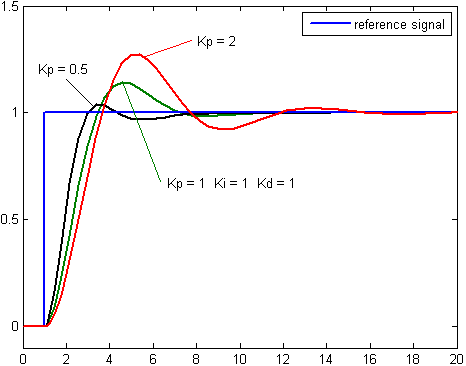
ผลอัตราขยายสัดส่วนที่สูงค่าความ ผิดพลาดก็จะเปลี่ยนแปลงมากเช่นกัน แต่ถ้าสูงเกินไประบบจะไม่เสถียรได้ ในทางตรงกันข้าม ผลอัตราขยายสัดส่วนที่ต่ำ ระบบควบคุมจะมีผลตอบสนองต่อกระบวนการน้อยตามไปด้วย | ||
เทอมปริพันธ์ (เมื่อรวมกับเทอมสัดส่วน) จะเร่งกระบวนการให้เข้าสู่จุดที่ต้องการและขจัดความผิดพลาดที่เหลืออยู่ที่ เกิดจากการใช้เพียงเทอมสัดส่วน แต่อย่างไรก็ตาม เทอมปริพันธ์เป็นการตอบสนองต่อความผิดพลาดสะสมในอดีต จึงสามารถทำให้เกิดโอเวอร์ชูตได้ (ข้ามจุดที่ต้องการและเกิดการหันเหไปทางทิศทางอื่น)
| ||
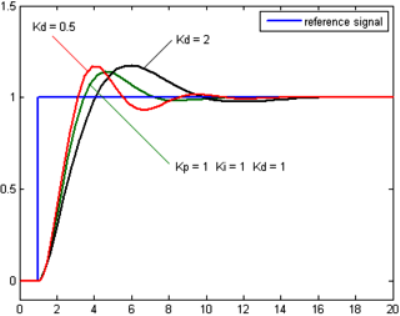
เทอมอนุพันธ์จะชะลออัตราการเปลี่ยนแปลงของสัญญาณขาออกของระบบควบคุมและ ด้วยผลนี้จะช่วยให้ระบบควบคุมเข้าสู่จุดที่ต้องการ ดังนั้นเทอมอนุพันธ์จะใช้ในการลดขนาดของโอเวอร์ชูตที่เกิดจาเทอมปริพันธ์และ ทำให้เสถียรภาพของการรวมกันของระบบควบคุมดีขึ้น แต่อย่างไรก็ตามอนุพันธ์ของสัญญาณรบกวนที่ถูกขยายในระบบควบคุมจะไวมากต่อการ รบกวนในเทอมของความผิดพลาดและสามารถทำให้กระบวนการไม่เสถียรได้ถ้าสัญญาณ รบกวนและอัตราขยายอนุพันธ์มีขนาดใหญ่เพียงพอ
|
ผลรวม
เทอมสัดส่วน, ปริพันธ์, และอนุพันธ์ จะนำมารวมกันเป็นสัญญาณขาออกของการควบคุมแบบ PID กำหนดให้ u(t) เป็นสัญญาณขาออก สมการสุดท้ายของวิธี PID คือ:
รหัสเทียม
รหัสเทียม (อังกฤษ: pseudocode) ของ ขั้นตอนวิธีระบบควบคุมพีไอดี โดยอยู่บนสมมุติฐานว่าตัวประมวลผลประมวลผลแบบขนานอย่งสมบรูณ์แบบ เป็นดังต่อไปนี้
previous_error = setpoint - actual_position integral = 0 start: error = setpoint - actual_position integral = integral + (error*dt) derivative = (error - previous_error)/dt output = (Kp*error) + (Ki*integral) + (Kd*derivative) previous_error = error wait(dt) goto start |
การปรับจูน
การปรับจูนด้วยมือ
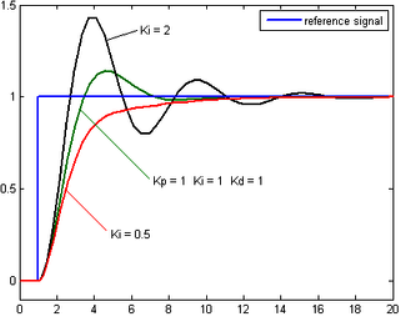
ถ้าระบบยังคงทำงาน ขั้นแรกให้ตั้งค่า Ki และ Kd เป็นศูนย์ เพิ่มค่า Kp จนกระทั่งสัญญาณขาออกเกิดการแกว่ง (oscillate) แล้วตั้งค่า Kp ให้เหลือครึ่งหนึ่งของค่าที่ทำให้เกิดการแกว่งสำหรับการตอบสนองชนิด "quarter amplitude decay" แล้วเพิ่ม Ki จนกระทั่งออฟเซตถูกต้องในเวลาที่พอเพียงของกระบวนการ แต่ถ้า Ki มากไปจะทำให้ไม่เสถียร สุดท้ายถ้าต้องการ ให้เพิ่มค่า Kd จนกระทั่งลูปอยู่ในระดับที่ยอมรับได้ แต่ถ้า Kd มากเกินไปจะเป็นเหตุให้การตอบสนองและโอเวอร์ชูตเกินยอมรับได้ ปกติการปรับจูน PID ถ้าเกิดโอเวอร์ชูตเล็กน้อยจะช่วยให้เข้าสู่จุดที่ต้องการเร็วขึ้น แต่ในบางระบบไม่สามารถยอมให้เกิดโอเวอร์ชูตได้ และถ้าค่า Kp น้อยเกินไปก็จะทำให้เกิดการแกว่ง
| ตัวแปร | ช่วงเวลาขึ้น (Rise time) | โอเวอร์ชูต (Overshoot) | เวลาสู่สมดุล (Settling time) | ความผิดพลาดสถานะคงตัว (Steady-state error) | เสถียรภาพ |
|---|---|---|---|---|---|
| Kp | ลด | เพิ่ม | เปลี่ยนแปลงเล็กน้อย | ลด | ลด |
| Ki | ลด | เพิ่ม | เพิ่ม | ลดลงอย่างมีนัยสำคัญ | ลด |
| Kd | ลดลงเล็กน้อย | ลดลงเล็กน้อย | ลดลงเล็กน้อย | ตามทฤษฏีไม่มีผล | ดีขึ้นถ้า Kd มีค่าน้อย |
วิธีการ Ziegler–Nichols
วิธีการนี้นำเสนอโดย John G. Ziegler และ Nathaniel B. Nichols ในคริสต์ทศวรรษที่ 1940 ขั้นแรกให้ตั้งค่า Ki และ Kd เป็นศูนย์ เพิ่มอัตราขยาย P สูงที่สุด, Ku , จนกระทั่งเริ่มเกิดการแกว่ง นำค่า Ku และค่าช่วงการแกว่ง Pu มาหาค่าตัวแปรที่เหลือดังตาราง:
| Control Type | Kp | Ki | Kd |
|---|---|---|---|
| P | 0.50Ku | - | - |
| PI | 0.45Ku | 1.2 Kp/Pu | - |
| PID | 0.60Ku | 2 Kp/Pu. | KpPu/8 |
อ้างอิง ขอขอบคุณสำหรับข้อมูลจาก : http://www.9engineer.com/index.php?m=article&a=show&article_id=2311
ช่องทางการติดต่อ
fb : @GreatOrientalTrading
line@ : @gotrading
Mobile : 097-3619703
Tel : 074-300212-4
Our Customer






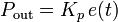
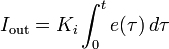
 : ตัวแปรปริพันธ์หุ่น
: ตัวแปรปริพันธ์หุ่น